EngiBench: A Benchmark for Evaluating Large Language Models on Engineering Problem Solving
We present EngiBench, a comprehensive benchmark for evaluating large language models on engineering problem solving across multiple disciplines. EngiBench covers diverse engineering domains and provides standardized evaluation metrics for assessing LLM capabilities in technical problem-solving tasks.
Key Findings
Our comprehensive evaluation of LLMs on EngiBench reveals critical insights about their engineering problem-solving capabilities across different complexity levels.
- Model Stratification and Design Validation: Performance shows a clear downward trend from Level 1 to Level 3, demonstrating the effectiveness of the hierarchical difficulty design.
- Evaluating High-Level Engineering Reasoning: At Level 3, models struggle with open-ended and underspecified tasks and score well below human experts (8.58), underscoring current limitations in high-level reasoning.
- Smaller-Scale LLMs Struggle with Complex Tasks: As task complexity increases, performance disparities widen—small models fall below 40% on Level 2 and under 4.0 on Level 3, while top models exceed 80% accuracy on Level 2.
- Robustness and Contamination Risk: Perturbed variants cause sharp accuracy drops (e.g., −9.3%, −11.4%, −8.3%), revealing reliance on superficial pattern matching rather than robust reasoning.
Benchmark Design
EngiBench employs a systematic three-level hierarchical design to comprehensively evaluate engineering problem-solving capabilities. Each level targets specific cognitive skills, from foundational knowledge retrieval to complex open-ended modeling, while four core capability dimensions ensure thorough assessment across diverse engineering scenarios.
Three-Level Hierarchical Structure
Foundational Knowledge Retrieval
Apply basic engineering concepts or standard formulas to structured problems via single-step computation.
Contextual Reasoning
Perform multi-step reasoning under well-defined constraints by integrating conditions and domain knowledge.
Open-ended Modeling
Solve open-ended, real-world problems through information extraction, trade-off reasoning, and uncertainty handling.
Four Core Capability Dimensions
Information Extraction
Identify and extract relevant information from complex or redundant problem descriptions.
Domain-specific Reasoning
Apply specialized engineering principles and structured knowledge to guide inference and solution formulation.
Multi-objective Decision Making
Make justified trade-offs between competing objectives in the absence of a single optimal solution.
Uncertainty Handling
Ensure solution robustness by reasoning under incomplete, variable, or ambiguous real-world conditions.
Dataset Construction
EngiBench is systematically constructed through diverse data sources and problem variants to ensure comprehensive evaluation of engineering problem-solving capabilities across different contexts and complexity levels.
Data Sources
EngiBench collects problems from three main sources to capture the diversity of real-world engineering challenges.
Public Benchmarks
Tasks adapted from MMLU, GSM8k, MATH, Omni-MATH, Big-Math, Orca-Math, HARP, AMC-AIME, etc.
University Resources
Authorized teaching materials and structured engineering exercises.
Modeling Competitions
43 open-ended problems from competitions (2010–2024), evaluated using expert-designed rubrics.
Problem Variants
Each problem is systematically rewritten to enable fine-grained capability analysis:
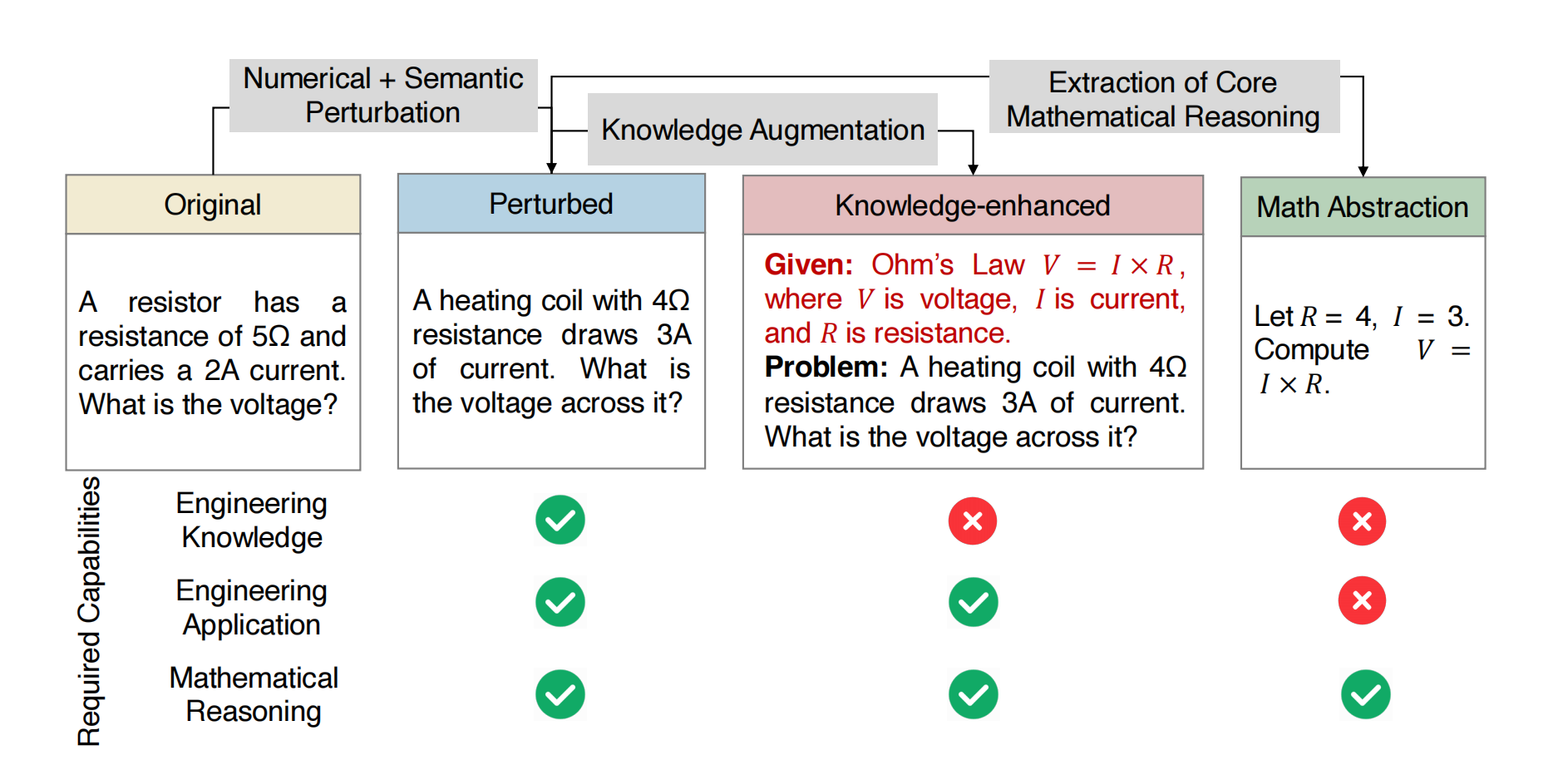
Original
The unmodified engineering problem.
Perturbed
Numerical and semantic changes to test robustness and avoid data overlap.
Knowledge-enhanced
Adds explicit formulas, constants, or definitions to check whether errors stem from missing knowledge.
Math Abstraction
Removes engineering context, reducing the problem to pure symbolic computation to test mathematical reasoning.
Performance for Level 1 & Level 2 Tasks
Our evaluation reveals significant performance variations across models and problem variants for foundational and contextual reasoning tasks.
- Knowledge Enhancement Benefits: Adding explicit domain knowledge significantly improves model accuracy across all levels, especially for weaker models. Models perform consistently better on knowledge-enhanced variants than on perturbed inputs.
- Math Abstraction Advantage: LLMs' performance further improves when problems are abstracted into symbolic mathematical form, eliminating engineering context. Most models achieve their highest accuracy under this variant, particularly smaller-scale LLMs that struggle with contextual interpretation.
- Small Model Instability: Smaller-scale LLMs exhibit significantly greater performance variation across different input versions, revealing their limited generalization and unstable reasoning processes. For example, Qwen2.5-7B drops by 11.4% under the perturbed version, but gains 16.6% when explicit domain knowledge is added.
- Large Model Robustness: Top-performing models like Gemini 2.5 Flash remain largely stable, with only minimal changes relative to their perturbed performance (-1.2%, +2.4%, and +0.1% respectively), highlighting that smaller-scale models are sensitive to input formulation and often rely on surface patterns rather than consistent, context-aware reasoning.
Performance for Level 3 Tasks
Our analysis of Level 3 tasks reveals the relationship between overall performance and domain-specific capabilities, highlighting the challenges models face in open-ended engineering problem solving.
- Strong Performance Correlation: Models with higher average accuracy (Level 1 & 2) generally achieve better Level 3 scores, indicating that foundational skills are crucial for complex problem-solving capabilities.
- Domain-Specific Variations: The heatmap reveals significant performance variations across different engineering domains, with some models excelling in specific areas while struggling in others.
- Open-ended Challenge: Even top-performing models like GPT-4.1 and Claude 3.7 Sonnet show substantial performance drops in Level 3 tasks, highlighting the difficulty of open-ended engineering reasoning.
- Model Stratification: Clear performance tiers emerge, with larger models consistently outperforming smaller variants across all domains, emphasizing the importance of model scale for complex reasoning tasks.
Dataset Statistics
EngiBench consists of comprehensive engineering problems spanning multiple disciplines including mechanical, electrical, chemical, civil, and computer engineering. The benchmark provides diverse problem types with varying difficulty levels to thoroughly evaluate LLM capabilities.
EngiBench covers multiple engineering disciplines and problem types to comprehensively evaluate LLM capabilities:
- Chemical & Biology: Chemical reactions, molecular calculations, and biological processes
- Physical & Structural: Mechanics, thermodynamics, and structural analysis across various engineering contexts
- Ocean Engineering: Marine and coastal engineering problems
- Multi-level Difficulty: Problems ranging from Level 1 (basic) to Level 3 (advanced modeling)
- Diverse Problem Formats: Including original problems, converted versions, and knowledge-enhanced variants
Conclusions and Insights
Based on our comprehensive evaluation using EngiBench, we draw key conclusions regarding the current capabilities and limitations of LLMs in engineering problem solving.
- Engineering problems require diverse skill sets including mathematical reasoning, domain knowledge, and practical application abilities.
- LLM performance varies significantly across different engineering disciplines, with some domains proving more challenging than others.
- Problem complexity and the need for multi-step reasoning present significant challenges for current LLMs.
- Knowledge enhancement and problem reformulation can improve LLM performance on engineering tasks.
Dataset Examples
This section showcases several examples from EngiBench across different engineering domains and difficulty levels. Explore the dataset at Hugging Face.
Citation
@article{engibench2025,
title={EngiBench: A Benchmark for Evaluating Large Language Models on Engineering Problem Solving},
author={Xiyuan Zhou and Xinlei Wang and Yirui He and Yang Wu and Ruixi Zou and Yuheng Cheng and Yulu Xie and Wenxuan Liu and Huan Zhao and Yan Xu and Jinjin Gu and Junhua Zhao},
journal={arXiv},
year={2025},
}



 Code
Code
 Dataset
Dataset